Uncertainty can adversely affect the operation of hydraulic and air systems. Understanding the flow characteristics requires essential mathematical tools, with one of them being Darcy’s equation which articulates the relationship between viscosity (fluid type & operating temperature – 𝜇), flow rate (Q) and mesh parameters such as its cross section of filtration (A), its open area and aperture (k) and thickness (L) with a friction factor.
One problem with the Darcy Equation is the difficulty in predicting a medium’s absolute permeability without the proper testing equipment. A method to complete this is through the use of the empirical formula commonly called the Kozeny-Carman approximation. A deep understanding of the theory enables us to not only have an educated guess at the specifying the correct mesh in the first place but to also be aware of the variables at play to efficiently allow us to solve complex problems to meet exacting requirements.
The Integral Form of Darcy's Equation
The integral form of Darcy’s Law permits calculating pressure drops over varying pipe sections:
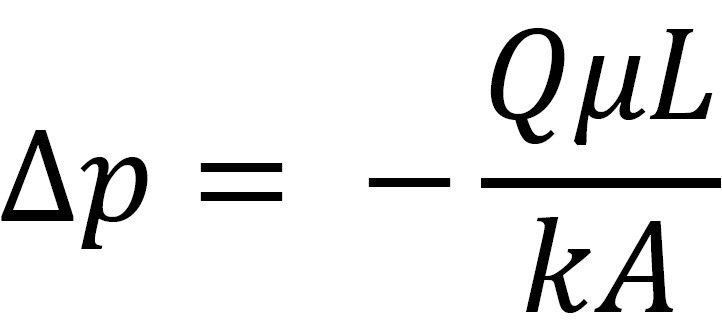

- ‘∆P’ equals pressure drop across your last chance filter
- ‘μ’ stands representing dynamic viscosity involved filtrate fluid
- ‘κ’ symbolises last chance filter’s absolute permeability
- ‘Q’ indicates local flow rate
- ‘A’ last chance filters active filtration area
Estimating Permeability: The Kozenv-Carman Relation
κ = d² φ³ / 180(1-φ)²
- ‘d’ signifies reference particle diameter (often median diameter an ideal selection)
- ‘φ’ denotes porosity measurement obtained via visual inspection or simple calculation methods.
By the way, the equations expressed here have their own limitations. For example, Darcy’s Law assumes a laminar flow and homogeneous isotropic fluid. If you need further help with these calculations, please get in touch.

